Ben Laurie and Matasano Chargen describe a significant attack on RSA signature implementation (not the algorithm itself). Quoting from Matasano:
Bell Labs crypto shaolin Daniel Bleichenbacher disclosed a freaky attack on RSA signature implementations that may, under some common circumstances, break SSL/TLS.
Do I have your attention? Good, because this involves PKCS padding, which is not exciting. Bear with me.
RSA signatures use a public signing keypair with a message digest (like SHA1) to stamp a document or protocol message. In RSA, signing and verification are analogs of decryption and encryption. To sign a message, you:
- Hash it
- Expand the (short) hash to the (long) size of the RSA modulus
- Convert that expansion to a number
- RSA decrypt the number
- Convert that to a series of bytes, which is your signature.
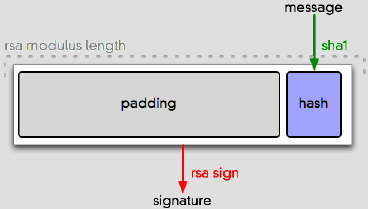
It’s step 2 we care about here. It’s called “paddingâ€. You need it because RSA wants to encrypt or decrypt something that is the same size as the RSA key modulus.
There are a bunch of different ways to pad data before operating on it, but the one everyone uses is called PKCS#1 v1.5 (technically, EMSA-PKCS1-V1_5-ENCODE). It involves tacking a bunch of data in front of your hash, enough to pad it out to the size of the modulus:
Note the order and placement of those boxes. They’re all variable length. Let’s call that out:
The two big goals of a padding scheme are (a) expanding messages to the modulus length and (b) making it easy to correctly recover the message bytes later, regardless of what they are. This padding scheme is designed to make that straightforward. The padding bytes are clearly marked (“00 01â€, which tells you that PKCS#1 v1.5 is in use), terminated (with a 00, which cannot occur in the padding), and followed by a blob of data with a length field. This whole bundle of data is what RSA works on.
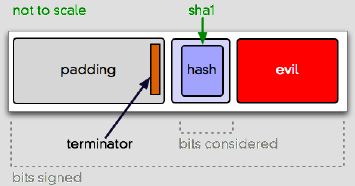
The problem is, despite all the flexiblity PKCS#1 v1.5 gives you, nobody expects you to ever use any of it. In fact, a lot of software apparently depends on data being laid out basically like the picture above. But all the metadata in that message gives you other options. For instance:
For some RSA implementations, this could be an acceptable message layout. It’s semantically invalid, but can appear syntactically valid. And if you don’t completely unpack and check all the metadata in the signature, well, this can happen:
- Determine the padding from the fixed header bytes.
- Scan until the terminator.
- Scoop out the hash information.
- Use the hash to confirm you’re looking at the same message that the “signer†signed.
- Use the signature to confirm that a real “signer†signed it.
The problem is that this attack breaks the connection between (4) and (5). The hash, now “centered†instead of “right-justifiedâ€, doesn’t really mean anything, because the signature covers a bunch more bits.
This is all trivia without some value for “evil†that lets you substitute an arbitrary message hash (and thus an arbitrary message) into an otherwise valid-looking signature. Enter Bleichenbacher’s attack.
RSA takes parameters, one of which is a “public exponentâ€, which is part of the public key. If that exponent is “3â€, which it often is, an attacker can exploit broken signature validation code to forge messages. The math here, which Bleichenbacher claims is simple enough to do with a pencil and paper, gets a bit hairy for me (I lose it at polynomials). Dino explains it better than I do. The long and the short of it is, you validate an RSA signature by computing:
s ^ e = m (mod n)(where “e†is the public exponent, “n†is the public modulus, and “s†is the signature) and verifying that you get the same result as applying steps (1) and (2) from the signature process yourself. But:
- If the public exponent is “3â€, and
- you inject the right “evil†bits into the PKCS data to make it a perfect cube, then
- you can create a something that broken RSA will validate.
Good technical details in Hal Finney’s OpenPGP post (OpenPGP is not vulnerable). And a security advisory for OpenSSL (OpenSSL is vulnerable, through 0.9.8b).
Two things have gone wrong here:
- Implementations misparse signatures, assuming that a syntactically valid-looking hash is semantically operative.
- For the common RSA exponent parameter “3â€, there’s a straightforward way to manipulate a bogus signature to make it look valid.
My understanding is, the demonstrated attack sticks the evil bits outside of the DigestInfo (the hash data). The way I see the bug being described, broken implementations are just scanning the buffer without “fully decoding itâ€, implying that if they just validated the ASN.1 metadata against the signature buffer they’d be OK. That may be true, but it seems possible that a blind “memcmp†on an over-long SHA1 octet string, which would be ASN.1-valid and leave the Digest at the end of the buffer, could also trigger the same bug.
This is only a problem if:
- You’re running broken code
- You’re relying on certificate validation
- The certificates you’re validating use an exponent of “3â€
Unfortunately, although the default for OpenSSL is “65537†(no practical attack known for that), “3†is common alternative: it’s faster, especially in embedded environments. Ferguson and Schneier recommend it in Practical Cryptography. Checking the CA bundle for “curlâ€:
cat curl-ca-bundle.crt | grep Exponent | grep “: 3” | wc -lgives 6 hits, from Digital Signature Trust Co. and Entrust.net. Those same certs are in Firefox. Firefox doesn’t use OpenSSL; it uses NSS, and I don’t know if NSS is vulnerable. Here’s the code. I see it extracting a SHA1 hash’s worth of data, and don’t see it checking to make sure that date exhausts the buffer, but I don’t know the code well. Safari also depends on OpenSSL.
Correct me on any of these points and I’ll amend the post. I haven’t tested this (although Google Security did a proof of concept against OpenSSL that precipitated the advisory).
You should upgrade to the most recent OpenSSL. Bleichenbacher also recommended people stop using signing keys with a “3†exponent.